Home · Book Reports · 2019 · Godel, Escher, Bach - An Eternal Golden Braid

designates my notes. / designates important.

Thoughts

These thoughts were written over a year after I read the book and are thus not to be taken as the best representation of the work.

Before I get into the content of the book, I must say that the entire work is laced with excellent, laugh-out-loud, humor. For such a long work it is actually very easy to read and would suggest it to anyone interested in philosophy or the early days of artificial intelligence. That said, I don’t mean to imply that I agree with what is presented here, merely that it is certainly interesting.

Part 1

Right off the bat my alarm bells are already ringing when he mentions sexism and apologizes for using the word men. He goes on to talk about how men eat animals and we think they have ‘smaller’ souls than our, so we “extinguish the dim lights in the heads of these fractionally-souled beasts and to gobble down their once warm and wiggling, now chilled and stilled protoplasm with limitless gusto, and not to feel a trace of guilt while doing so.” It feels very “liberal” and goes on to address sexism in language like mankind. The author is a Stanford undergrad and did some short-lived graduate work at Berkeley.

This was a most interesting read. While I am skeptical of many of the arguments the author puts forth, I can not deny that reading this book was both intellectually stimulating and enjoyable. If nothing else, a look at the thoughts of an artificial intelligence researcher of the 1970’s was insightful given the prominence today of said field.

The book itself if constructed in a peculiar manner; each chapter is preceded by a dialog between a number of recurring characters, the primary ones being Achilles and the Tortoise, but also includes a few of their friends. These dialogs are, of course, inspired by Lewis Carroll’s ‘What the tortoise said to Achilles.’ While I was and am capable of delaying judgment based on this Carroll fandom, it can not be overstated how influential Carroll was to modern day oligarchs, not to mentioned his often unmentioned love of photographing children. If you ever wondered where his inspiration came for Alice, I’d suggest you do a little research yourself; it is more than shocking.

Back to the book. It begins by introducing the MU-puzzle, a light introduction to formal systems. I think this is a wonderful jumping off point as it pulls the reader in immediately involving them instead of (dis?) passionately preaching to them.

Next, another formal system the ‘p q -’ system is introduced. This is an extremely simple system that is isomorphic with addition. Again, I think the way that formal systems are introduced, gradually and approachable, is of great service to a lay reader.

Building on these formal systems the book then examines figure and ground, terms familiar to any artist readers. Here the work of M.C. Escher is used to show the difference between positive and negative space (figure and ground). A few images of alphabets where the letters are both figure and ground are used as examples. One is the Figure-Figure drawing where the figure and the ground are the same.

With this understanding of how the figure and the ground can define one another, the author turns back to formal systems. Can the true theorems and false theorems relate to one another in a figure/ground relationship? The ‘p q -’ system is modified to map onto multiplication and then used to build theorems for composites. The question then becomes: can we build on the negative space of composite theorem, to reveal the primes? The answer in this case is yes, but not all negative space gives rise to another system. What is not in a system (ground) will not always be the theorems of another system (figure).

This part of the book finishes up with a dialog about breaking phonographs and hidden messages in music/poetry before moving on to exploring the consistency and completeness of formal systems. It focuses on geometry: euclidean, non-euclidean, and absolute (4 postulate) geometry.

Next, in a section titled little harmonic labyrinth, the tortoise and Achilles go on nested adventures. Nested as in recursive. We are given some explanation as to what a base case is (“bottoming out”) and some well known examples (Fibonacci). Then the author looks at what a recursive program would look like if there was no base case.

Needless to say, there can be a trio of procedures which call one another, cyclically-and so on. There can be a whole family of RTN’s [recursive transitive network] which are all tangled up, calling each other and themselves like crazy. A program which has such a structure in which there is no single “highest level”, or “monitor”, is called a heterarchy (as distinguished from a hierarchy). The term is due, I believe, to Warren McCulloch, one of the first cyberneticists, and a reverent student of brains and minds.

You might well wonder whether such an intricate structure would ever show up in an experiment. Frankly, I would be the most surprised person in the world if Gplot came out of any experiment. The physicality of Gplot lies in the fact that it points the way to the proper mathematical treatment of less idealized problems of this SOI·t. In other words, Gplot is purely a contribution to theoretical physics, not a hint to experimentalists as to what to expect to see! An agnostic friend of mine once was so struck by Gplot’s infinitely many infinities that he called it “a picture of God”, which I don’t think is blasphemous at all.

Finally the topic of recursion is closed off by looking at recursive enumeration, a process where new things can emerge from old things that follow a fixed set of rules. This reminds me of Conway’s game of life.

In Canon by Intervallic Augmentation looks at messages and the levels of information contained within them. The example includes a jukebox with one record and many phonographs and discusses the frame, outer, and inner messages.

In Chromatic Fantasy, And Feud Tortoise contradicts himself and Achilles points it out, but Tortoise turns it back on him. Achilles feels bad. This leads into propositional calculus (logic) and its rules like and, or, not, and implies.

Within a system like this, if you can imagine a contradiction, the rules are in question (prudence). So (imprudence) don’t imaging contradictions.

As I take these notes, I think this is laying the foundation for being unable to prove a system from within itself.

The Crab Canon is basically same forward and backwards, absolutely delightful!

The next system explored is Typographical Number Theory, which has Propositional Calculus embedded in it.

Any system that is strong enough to prove TNT’s consistency is at least as strong as TNT itself. And so circularity is inevitable.

In A MU Offering zen koans and molecular biology are compared, which leads to discussion on Godel numbering, converting between systems, and isomorphic systems.

Part 2

Part 2 starts off with a more grounded look into things like programming languages, particularly machine and assembly language. There is a look at the hierarchy of computers with lots of comparisons to computers and brains hinting at AI. AI here is spoken as a computer that can program itself or understand the same data in two different contexts.

Examples of hierarchy, that can be thought of as levels which are sealed off from one another, are presented with simplicities in mind are given as sub-atomic, atomic, molecular, cellular, etc. This part reminds me of Koestler’s discussion on parts and whole in (I think) Act of Creation, but may have been The Ghost in the Machine.

I am also again reminded of Conway’s game of life during a discussion on epiphenomena, emergent phenomena from a system that is not specifically programmed into it.

In Ant Fugue we look at signals in an ant colony and ask if this is a kind of intelligence. Could you map any intelligence onto these signals, but not the individual ant? Is there a caste distribution of ants like a ‘brain state’? Are the building blocks are not necessary to describe the higher level?

Is it reasonable to compare ants and neurons? There are similar things happening already when we look at the isomorphic mapping from what you see into 2D electrical signals in the retina to 3D electrical signals farther back in the brain (lateral geniculate).

This gives rise to things like symbols and memory. We don’t remember things, but instead somehow electrical signals (symbols) can allow recall (memory). What about procedural vs. explicit knowledge. We know a mountain is bigger than a car not by rote memorization, but by deduction, procedurally.

Following the symbols and memory reasoning, there is an interesting comparing a trip via roads through cities to a thought and its neuropathways. The thoughts move along the roadways and the cities represent symbols. Each individual’s map will be different because we all know different things, but the bigger parts, like New York City or Chicago, will be omnipresent. This will allow us to communicate using those commonalities as landmarks.

This makes me think about how people so often “talk past” one another. If you don’t have these commonalities (in language) you won’t ever get anywhere. A simple example can be seen with the way people talk about (economic) inflation. The textbook definition would be an expanding monetary supply. This in turn will very likely lead to price increases to accommodate the large money supply. The problem is when people use the word inflation to mean rising prices. There are other reasons why prices might increase from forces that have nothing to do with actual inflation. This leads to an inability to communicate about inflation and possible price increases.

It doesn’t seem to be purposeful, but a few chapters later there is a discussion on supernatural numbers and the consequences of things like rational, irrational, negative, and imaginary numbers or the extending geometry in a non-Euclidean manner. This gives rise to the author talking about “abstract space” and how it is used in physics as if they were as real as actual reality.

This is interesting because the book was written in 1979 and it “predicted” the rise of theoretical physics. While theoretical physics isn’t brand new, I think it is safe to say there has been an explosion in the acceptance over the last 2 decades or so. I point to this with a twist on an old saying: “the math is not the territory.” I also think that what we are seeing now with people “living” online and likely soon in augmented/virtual reality, is a natural consequence of Kantian philosophy that will ultimately lead to the atomization of society to the sub-individual level. By sub-individual I mean that when people can’t even know/decide if they are boys or girls, or even humans, the atomization will be worse that if you were (or felt) merely isolated from the group, but you are effectively isolated from yourself.

Next we move back to comparing brains to programs. If we extend Godel’s theorem from TNT to TNT+G (etc), are humans as susceptible to Godel’s “trick” as any machine?

Lucas argues humans can always transcend the formal system that a computer must be bound by, but the author argues that eventually humans won’t be able to do so, at which point the machine is as powerful as a human. Both are not ‘all knowing’, but neither can know more. The author makes an analogy: some days you might be able to lift 250 pounds, others days not, but you will never lift 250 tons.

Basically the argument is that humans are simply very complex formal systems that, like their mechanical counterparts, won’t be able to step outside of themselves.

As much as humans try, we are still, for example, bound by the laws of physics, a higher (or lower) system that rules us.

This comparison continues into the molecular biology of cells, DNA, xRNA, and enzymes to computer hard/software systems like processors, programs, and interpreters.

The author claims that the substrate and the higher level symbols of the world, the mind, and the computer can be seen as partially isomorphic. This feels very close to: “as above, so below.”

This all leads up to a retro- and prospectus on artificial intelligence. How, as we build more complex and more feedback into our AI programs, they will appear to be a giant knot that we might not even understand. Could this unknowable knot give rise to “strange loops” that self-reference and might one day be called sentience? For my part, I am highly skeptical that anything like the Hollywood or Silicon Valley version of AI will ever exist. That said, I think the ability for programs that are extremely good at classification will ultimately be able to replace a lot of work that humans never imagined would be done by software.

The book ends on another humorous take on self-referentialism:

Author: I guess it all depends on how you look at it. But major or minor, I’d be most pleased to tell you how I braid the three together, Achilles. Of course, this project is not the kind of thing that one does in just one sitting-it might take a couple of dozen sessions. I’d begin by telling you the story of the Musical Offering, stressing the Endlessly Rising Canon, and-

Achilles: Oh, wonderful! I was listening with fascination to you and Mr. Crab talk about the Musical Offering and its story. From the way you two talk about it, I get the impression that the Musical Offering contains a host of formal structural tricks.

Author: After describing the Endlessly Rising Canon, I’d go on to describe formal systems and recursion, getting in some comments about figures and grounds, too. Then we’d come to self-reference and self- replication, and wind up with a discussion of hierarchical systems and the Crab’s Theme.

Further Reading

• Erving Goffman’s book Frame Analysis
  • advertising arms race, sounds very interesting
• Jauch’s four Dialogues in Are Quanta Real?

Exceptional Excepts

Typographical rules for manipulating numerals are actually arithmetical rules for operating on numbers.

This simple observation is at the heart of Godel’s method, and it will have an absolutely shattering effect. It tells us that once we have a Godel- numbering for any formal system, we can straightaway form a set of arithmetical rules which complete the Godel isomorphism. The upshot is thatwe can transfer the study of any formal system-in fact the study of all formal systems-into number theory.

By looking at things from the vast perspective of evolution, you can drain the whole colony of meaning and purpose.

The significance of the notion is shown by the following key fact: If you have a sufficiently powerful formalization of number theory, then Godel’s method is applicable, and consequently your system is incomplete. If, on the other hand, your system is not sufficiently powerful (i.e., not all primitive recursive truths are theorems), then your system is, precisely by virtue of that lack, incomplete. Here we have a reformulation of “Ganto’s Ax” in metamathematics: whatever the system does, Godel’s Ax will chop its head om Notice also how this completely parallels the high-fidelity-versus-low- fidelity battle in the Contracrostipunctus.

You fit your mathematics to the world, and not the other way around.

As the ordinals [names of infinities] get bigger and bigger, there are irregularities, and irregularities in the irregularities, and irregularities in the irregularities in the ir- regularities, etc. No single scheme, no matter how complex, can name all the ordinals. And from this, it follows that no algorithmic method can tell how to apply the method of Godel to all possible kinds of formal systems. And unless one is rather mystically inclined, therefore one must conclude that any human being simply will reach the limits of his own ability to Godelize at some point. From there on out, formal systems of that complexity, though admittedly incomplete for the Godel reason, will have as much power as that human being.

But-one should not consider TNT defective for that reason. If there is a defect anywhere, it is not in TNT, but in our expectations of what it should be able to do. Furthermore, it is helpful to realize that we are equally vulnerable to the word trick which Godel transplanted into mathematical formalisms: the Epimenides paradox. This was quite cleverly pointed out by C. H. Whitely, when he proposed the sentence “Lucas cannot consistently assert this sentence.” If you think about it, you will see that (1) it is true, and yet (2) Lucas cannot consistently assert it. So Lucas is also “incomplete” with respect to truths about the world. The way in which he mirrors the world in his brain structures prevents him from simultaneously being “consistent” and asserting that true sentence.But Lucas is no more vulnerable than any of us. He is just on a par with a sophisticated formal system.

Well, this is the kind of “heads-in-the-sand” argument which you have to be willing to stomach if you are bent on seeing men and women running ahead of computers in these intellectual battles.

one of the main theses of this book: that every aspect of thinking can be viewed as a high-level description of a system which, on a low level, is governed by simple, even formal, rules.

According to my hypothesis, then, imagery and analogical thought processes intrinsically require several layers of substrate and are therefore intrinsically non-skimmable. I believe furthermore that it is precisely at this same point that creativity starts to emerge

Table of Contents

• Preface (1999)

Part 1

• Introduction:A Musico-Logical Offering
• 01: The MU-puzzle
• 02: Meaning and Form in Mathematics
• 03: Figure and Ground
• 04: Consistency, Completeness, and Geometry
• 05: Recursive Structures and Processes
• 06: The Location of Meaning
• 07: The Propositional Calculus
• 08: Typographical Number Theory
• 09: Mumon and Godel

Part 2

• Prelude
• 10: Levels of Description, and Computer Systems
• 11: Brains and Thoughts
• 12: Minds and Thoughts
• 13: BlooP and FlooP and Gloop
• 14: On Formally Undecidable Propositions of TNT and Related Systems
• 15: Jumping Out of the System
• 16: Self-Rep and Self-Rep
• 17: Church, Turing, Tarski, and Others
• 18: Artificial Intelligence: Retrospects
• 19: Artificial Intelligence: Prospects
• 20: Strange Loops, Or Tangled Hierarchies

• Actual pages numbers.(part 2 is -1 page off)

· Preface (1999)

• By Douglas R. Hofstadter

page x:

• Godel set about showing the innate self reference in Russell and Whitehead’s Principia Mathematica.

page xi:

• In short, an “I” comes about - in my view, at least - via a kind of vortex whereby patterns in a brain mirror the brain’s mirroring of the world, and eventually mirror themselves, whereupon the vortex of “I” becomes a real, causal entity. For an imperfect but vivid concrete analogue to this curious abstract phenomenon, think of what happens when a 1V camera is pointed at a 1V screen so as to display the screen on itself (and that screen on itself, etc.)
• what in GEB I called a “self-engulfing television”, and in my later writings I sometimes call a “level-crossing feedback loop”.

page xii:

• Using ‘men’ to describe people is sexist. He apologizes for his use of the word ‘men’.

page xiii:

• as an undergraduate math major at Stanford and a few years later, in my short-lived career as a graduate student in math at Berkeley, I took several advanced logic courses, but to my bitter disappointment, all of them were arcane, technical, and utterly devoid of the magic I’d known in Nagel and Newman.

page xv:

• the “Yom Kippur war”, which made a very deep impression on me.

• shamelessly borrowing Lewis Carroll’s odd couple of Achilles and the Tortoise, whose droll personalities amused me no end

page xx:

• GEB remained a book with a deep sexist bias sewn into its fabric. Interestingly, it is a bias that very few readers, females or males, have commented on (which in tum supports my belief that these kinds of things are very subtle and insidious, and escape nearly everyone’s perception).

• Or people don’t care about the sex of characters in a book? (until the media/education system brainwashes them)

page xii:

• A few months later, I received a pair ofreviews published in successive issues of Humanisme, an obscure journal put out by the Society of French Freemasons. Both had issued from the pen of one author, Alain Houlou, and I tackled them with interest. The first one was quite lengthy and, like that in Le Monde, glowed with praise; I was gratified and grateful. I then went on to the second review, which started out with the poetic phrase Apres les roses, les epines … (“After roses, thorns … “), and which then proceeded for several pages, to my amazement, to rip GEB apart as un piege tres grave (“a very dangerous trap”) in which the mindless bandwagon of Zen Buddhism was eagerly jumped on, and in which a rabidly antiscientific, beatnik-influenced, hippie-like irrationality typical of American physicists was embraced as the supreme path to enlightenment, with the iconoclastic Zen-influenced American composer John Cage as the patron saint of it all. Twentieth-anniversary Preface P-17 All I could do was chuckle, and throw my hands up in bewilderment at these Tati-esque vacarmes de monsieur Houlou. Somehow, this reviewer saw me praising Cage to the skies (“Godel, Escher, Cage”?) and managed to read into my coy allusions to and minor borrowings from Zen an uncritical acceptance thereof, which in fact is not at all my stance. As I declare at the start of Chapter 9, I find Zen not only confusing and silly, but on a very deep level utterly inimical to my core beliefs. However, I also find Zen’s silliness - especially when it gets really silly - quite amusing, even refreshing, and it was simply fun for me to sprinkle a bit of Eastern spice into my basically very Western casserole. However, my having sprinkled little traces of Zen here and there does not mean that I am a Zen monk in sheep’s clothing. As for John Cage, for some odd reason I had felt very sure, up till reading Houlou’s weird about-face, that in my “Canon by Intervallic Augmentation” and the chapter that follows it, I had unambiguously heaped scorn on Cage’s music, albeit in a somewhat respectful manner. But wait, wait, wait - isn’t “heaping respectful scorn” not a contradiction in terms, indeed a patent impossibility? And doesn’t such coy flirting with self- contradiction and paradox demonstrate, exactly as Houlou claims, that I am, deep down, both antiscientific and pro-Zen, after all? Well, so be it.

• 2 reviews by the same author; Society of Freemasons. Controlled opposition? Promotion through controversy?

· Introduction:A Musico-Logical Offering

page 17:

• That paradox is the so-called Epimenides paradox, or liar paradox. Epimenides was a Cretan who made one immortal statement: “All Cretans are liars.” A sharper version of the statement is simply “I am lying”; or, “This statement is false”. It is that last version which I will usually mean when I speak of the Epimenides paradox. It is a statement which rudely violates the usually assumed dichotomy of statements into true and false, because if you tentatively think it is true, then it immediately backfires on you and makes you think it is false. But once you’ve decided it is false, a similar backfiring returns you to the idea that it must be true. Try it!

• Godel’s Theorem appears as Proposition VI in his 1931 paper “On Formally Undecidable Propositions in Principia Mathematica and Related Systems I.” It states:

• To every w-consistent recursive class K of formulae there correspond recursive class-signs r, such that neither v Gen r nor Neg (v Gen r) belongs to Fig (K) (where v is the free variable of r).

• Actually, it was in German, and perhaps you feel that it might as well be in German anyway. So here is a paraphrase in more normal English:

-All consistent axiomatic formulations of number theory include undecidable propositions.

Three-Part Invention

page 29:

• Achilles, Tortoise, Zeno. A flag and a race.

· 01: The MU-puzzle

page 34:

start with 'MI'; try to reach 'MU'

RULE I: If you possess a string whose last letter is I, you can add on a U at
the end.

RULE II: Suppose you have Mx. Then you may add Mxx to your collection.

What I mean by this is shown below, in a few examples.
From MIU, you may get MIUIU.
From MUM, you may get MUMUM.
From MU, you may get MUU.

RULE III: If III occurs in one of the strings in your collection, you may make
a new string with U in place of III.

Examples:
From UMIIIMU, you could make UMUMU.
From MIIII, you could make MIU (also MUI).
From IIMII, you can't get anywhere using this rule.
(The three I's have to be consecutive.)
From MIII, make MU.

RULE IV: If UU occurs inside one of your strings, you can drop it.

Examples:
From UUU, get U.
From MUUUIII, get MUIII.


Solution?
No solution

page 37:

• to take a silly example, a car will never pick up the idea, no matter how much or how well it is driven, that it is supposed to avoid other cars and obstacles on the road; and it will never learn even the most frequently traveled routes of its owner. The difference, then, is that it is possible for a machine to act unobservant; it is impossible for a human to act unobservant. Notice I am not saying that all machines are necessarily incapable of making sophisticated observa- tions; just that some machines are. Nor am I saying that all people are always making sophisticated observations; people, in fact, are often very unobservant. But machines can be made to be totally unobservant; and people cannot.

• there are cases where only a rare individual will have the vision to perceive a system which governs many peoples’ lives, a system which had never before even been recognized as a system; then such people often devote their lives to convincing other people that the system really is there, and that it ought to be exited from!

page 41:

• If there is a test for theoremhood, a test which does always terminate in a finite amount of time, then that test is called a decision procedure for the given formal system.

• the difference between the set of axioms and the set of theorems: the former always has a decision procedure, but the latter may not.

Two-Part Invention

page 43:

• or, What the Tortoise Said to Achilles by Lewis Carroll

· 02: Meaning and Form in Mathematics

page 46:

• The Carrollian Dialogue, with its wit subtracted out, still leaves a deep philosophical problem: Do words and thoughts follow formal rules, or do they not? That problem is the problem of this book.

page 49:

• “isomorphism” was defined as an information- preserving transformation.

page 53:

• Can all of reality be turned into a formal system? In a very broad sense, the answer might appear to be yes. One could suggest, for instance, that reality is itself nothing but one very complicated formal system. Its symbols do not move around on paper, but rather in a three- dimensional vacuum (space); they are the elementary particles of which everything is composed. (Tacit assumption: that there is an end to the descending chain of matter, so that the expression “elementary particles” makes sense.) The “typographical rules” are the laws of physics, which tell how, given the positions and velocities of all particles at a given instant, to modify them, resulting in a new set of positions and velocities belonging to the “next” instant. So the theorems of this grand formal system are the possible configurations of particles at different times in the history of the universe. The sole axiom is (or perhaps, was) the original configuration of all the particles at the “beginning of time”.

Sonata for Unaccompanied Achilles

· 03: Figure and Ground

Contracrostipunctus

page 81:

• there are so many clever ways of hiding things in music …

• … or in poems. Poets used to do very similar things, you know (though it’s rather out of style these days). For instance, Lewis Carroll often hid words and names in the first letters (or characters) of the successive lines in poems he wrote. Poems which conceal messages that way are called “acrostics”.

page 85:

· 04: Consistency, Completeness, and Geometry

page 98:

• pointless lines

page 101:

• Consistency: when every theorem, upon interpretation, comes out true (in some imaginable world).

• Completeness: when all statements which are true (in some imaginable world), and which can be expressed as well-formed strings of the system, are theorems.

Little Harmonic Labyrinth

· 05: Recursive Structures and Processes

page 134:

• Needless to say, there can be a trio of procedures which call one another, cyclically-and so on. There can be a whole family of RTN’s [recursive transitive network] which are all tangled up, calling each other and themselves like crazy. A program which has such a structure in which there is no single “highest level”, or “monitor”, is called a heterarchy (as distinguished from a hierarchy). The term is due, I believe, to Warren McCulloch, one of the first cyberneticists, and a reverent student of brains and minds.

page 141:

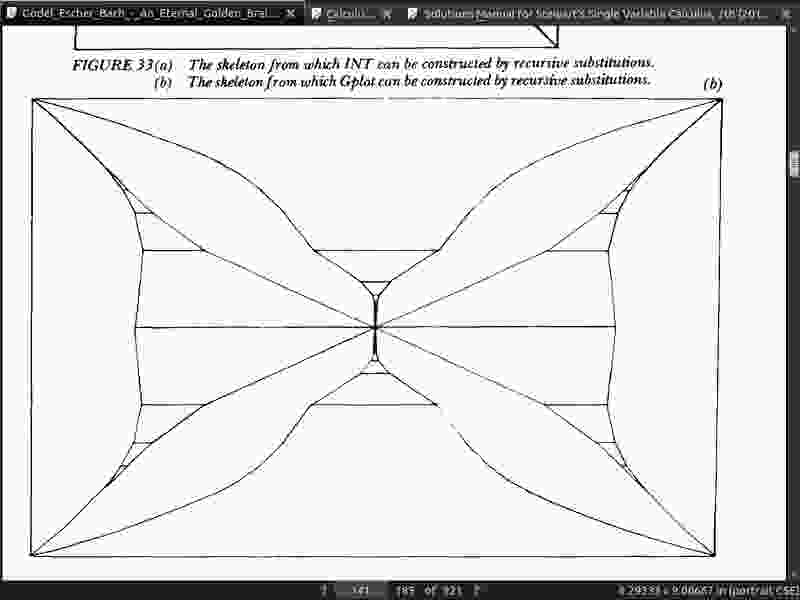
page 142:

• You might well wonder whether such an intricate structure would ever show up in an experiment. Frankly, I would be the most surprised person in the world if Gplot came out of any experiment. The physicality of Gplot lies in the fact that it points the way to the proper mathematical treatment of less idealized problems of this SOI·t. In other words, Gplot is purely a contribution to theoretical physics, not a hint to experimentalists as to what to expect to see! An agnostic friend of mine once was so struck by Gplot’s infinitely many infinities that he called it “a picture of God”, which I don’t think is blasphemous at all.

page 144:

page 152:

• Recursive enumeration is a process in which new things emerge from old things by fixed rules.

Canon by Intervallic Augmentation

· 06: The Location of Meaning

page 158:

• In this Chapter, I want to present the case for the universality of at least some messages, without, to be sure, claiming it for all messages.

page 172:

• consider a meteorite which, instead of deciphering the outer-space Bach record, punctures it with colossal indifference, and continues in its merry orbit. It has interacted with the record in a way which we feel disregards the record’s meaning. Therefore, we might well feel tempted to call the meteorite “stupid”. But perhaps we would thereby do the meteorite a disservice. Perhaps it has a “higher intelligence” which we in our Earth chauvinism cannot perceive, and its interaction with the record was a manifestation of that higher intelligence. Perhaps, then, the record has a “higher meaning”-totally different from that which we attribute to it; perhaps its meaning depends on the type of intelligence perceiving it. Perhaps. It would be nice if we could define intelligence in some other way than “that which gets the same meaning out of a sequence of symbols as we do”.

page 174:

• A [John] Cage piece has to be taken in a large cultural setting-as a revolt against certain kinds of traditions.

• It is fair to say, then, that an isolated record of John Cage’s music does not have an intrinsic meaning.

page 175:

• On the other hand, to appreciate Bach requires far less cultural knowledge. This may seem like high irony, for Bach is so much more complex and organized, and Cage is so devoid of intellectuality. But there is a strange reversal here: intelligence loves patterns and balks at randomness. For most people, the randomness in Cage’s music requires much explanation; and even after explanations, they may feel they are missing the message-whereas with much of Bach, words are superfluous. In that sense, Bach’s music is more self-contained than Cage’s music. Still, it is not clear how much of the human condition is presumed by Bach.

• The general question which we are facing, and which is very similar to the questions inspired by the two plaques, is this: “How much of the context necessary for its own understanding is a message capable of restoring?” We can now revert to the original biological meanings of “genotype” and “phenotype”-DNA and a living organism-and ask similar questions. Does DNA have universal triggering power? Or does it need a “biojukebox” to reveal its meaning? Can DNA evoke a phenotype without being embedded in the proper chemical context? To this question the answer is no-but a qualified no. Certainly a molecule of DNA in a vacuum will not create anything at all. However, if a molecule of DNA were sent out to seek its fortune in the universe, as we imagined the BACH and the CAGE were, it might be intercepted by an intelligent civilization. They might first of all recognize its frame message. Given that, they might go on to try to deduce from its chemical structure what kind of chemical environment it seemed to want, and then supply such an environment. Successively more refined attempts along these lines might eventually lead to a full restoration of the chemical context necessary for the revelation of DNA’s phenotypical meaning. This may sound a little implausible, but if one allows many millions of years for the experiment, perhaps the DNA’s meaning would finally emerge.

Chromatic Fantasy, And Feud

· 07: The Propositional Calculus

page 186:

• The symbol ‘v’ represents the word ‘or’ (‘vel’ is a Latin word for ‘or’). The ‘or’ that is meant is the so-called inclusive ‘or’, which means that the interpretation of < xv y> is “either x or y- or both”.

page 192:

• This little debate shows the difficulty of trying to use logic and reasoning to defend themselves. At some point, you reach rock bottom, and there is no defense except loudly shouting, “I know I’m right!” Once again, we are up against the issue which Lewis Carroll so sharply set forth in his Dialogue: you can’t go on defending your patterns of reasoning forever.There comes a point where faith takes over.

page 196:

• If you found a contradiction in your own thoughts, it’s very unlikely that your whole mentality would break down. Instead, you would probably begin to question the beliefs or modes of reasoning which you felt had led to the contradictory thoughts. In other words, to the extent you could, you would step out of the systems inside you which you felt were responsible for the contradiction, and try to repair them. One of the least likely things for you to do would be to throw up your arms and cry, “Well, I guess that shows that I believe everything now!” As a joke, yes-but not seriously.

Crab Canon

• This is basically same forward and backwards, absolutely delightful!

· 08: Typographical Number Theory

page 222:

• A system is w-incomplete (omega-incomplete) if all the strings in a pyramidal family are theorems, but the universally quantified summarizing string is not a theorem. Incidentally, the negation of the above summarizing string- ~Va:(O+a)=a [all a]-is also a nontheorem of TNT. This means that the original string is undecidable within the system.

page 230:

• Any system that is strong enough to prove TNT’s consistency is at least as strong as TNT itself. And so circularity is inevitable.

• Essentially what Godel showed.

A MU Offering

· 09: Mumon and Godel

page 264:

• Typographical rules for manipulating numerals are actually arithmetical rules for operating on numbers.

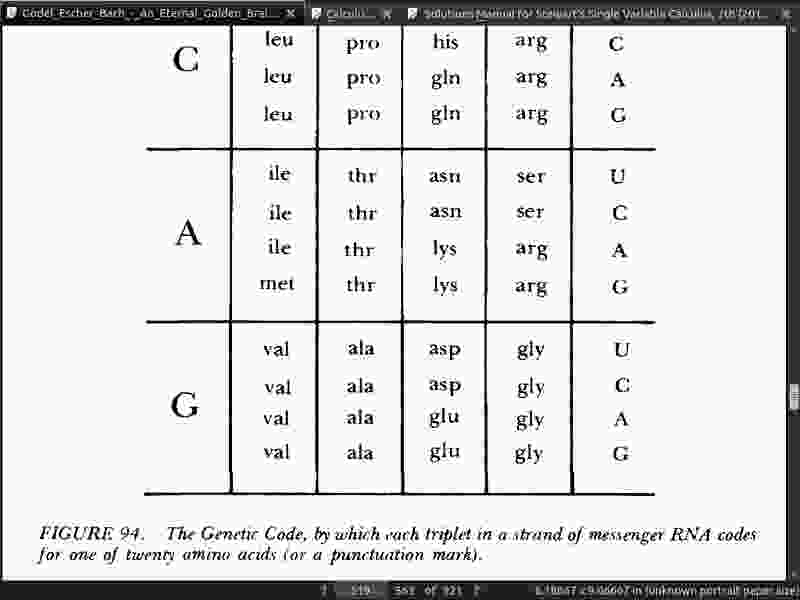
• This simple observation is at the heart of Godel’s method, and it will have an absolutely shattering effect. It tells us that once we have a Godel- numbering for any formal system, we can straightaway form a set of arithmetical rules which complete the Godel isomorphism. The upshot is thatwe can transfer the study of any formal system-in fact the study of all formal systems-into number theory.

Part 2

· Prelude

· 10: Levels of Description, and Computer Systems

page 301:

• To suggest ways of reconciling the software of mind with the hardware of brain is a main goal of this book.

page 303:

• However, there are more pathological cases, such as the proton and neutron seen as systems themselves. Each of them has been hypothesized to be constituted from a trio of “quarks”-hypothetical particles which can be combined in twos or threes to make many known fundamental particles. However, the interaction between quarks is so strong that not only can they not be seen inside the proton and neutron, but they cannot even be pulled out at all! Thus, although quarks help to give a theoretical understanding of certain properties of protons and neutrons, their own existence may perhaps never be independently established. Here we have the antithesis of a “nearly decomposable system”-it is a system which, if anything, is “nearly indecomposable”. Yet what is curious is that a quark-based theory of protons and neutrons (and other particles) has considerable explanatory power, in that many experimental results concerning the particles which quarks supposedly compose can be accounted for quite well, quantitatively, by using the “quark model”.

page 308:

• In coming Chapters, where we discuss the brain, we shall examine whether the brain’s top level-the mind-can be understood without understanding the lower levels on which it both depends and does not depend. Are there laws of thinking which are “sealed off” from the lower laws that govern the microscopic activity in the cells of the brain? Can mind be “skimmed” off of brain and transplanted into other systems? Or is it impossible to unravel thinking processes into neat and modular subsystems? Is the brain more like an atom, a renormalized electron, a nucleus, a neutron, or a quark? Is consciousness an epiphenomenon? To understand the mind, must one go all the way down to the level of nerve cells?

Ant Fugue

page 321:

• By looking at things from the vast perspective of evolution, you can drain the whole colony of meaning and purpose.

page 325:

Anteater: But you see, despite appearances, the ants are not the most important
feature. Admittedly, were it not for them, the colony wouldn't exist; but
something equivalent-a brain-can exist, ant-free.  So, at least from a
high-level point of view, the ants are dispensable.

Achilles: I'm sure no ant would embrace your theory with eagerness.

Anteater: Well, I never met an ant with a high-level point of view.

Crab: What a counterintuitive picture you paint, Dr. Anteater. It seems that,
if what you say is true, in order to grasp the whole structure, you have to
describe it omitting any mention of its fundamental building blocks.

Anteater: Perhaps I can make it a little clearer by an analogy. Imagine you
have before you a Charles Dick.ens novel.

Achilles: The Pickwick Papers-will that do?

Anteater: Excellently! And now imagine trying the following game: you must find
a way of mapping letters onto ideas, so that the entire Pickwick Papers makes
sense when you read it letter by letter.

Achilles: Hmm ... You mean that every time I hit a word such as "the", I have
to think of three definite concepts, one after another, with no room for
variation?

Anteater: Exactly. They are the 't'-concept, the 'h' -concept, and the 'e'
-concept-and every time, those concepts are as they were the pre- ceding time.

Achilles: Well, it sounds like that would turn the experience of "reading" The
Pickwick Papers into an indescribably boring nightmare. It would be an exercise
in meaninglessness, no matter what concept I associated with each letter.

Anteater: Exactly. There is no natural mapping from the individual letters into
the real world. The natural mapping occurs on a higher level- between words,
and parts of the real world. If you wanted to describe the book, therefore, you
would make no mention of the letter level.

Achilles: Of course not! I'd describe the plot and the characters, and so
forth.

Anteater: So there you are. You would omit all mention of the building blocks,
even though the book exists thanks to them. They are the medium, but not the
message.

page 334:

· 11: Brains and Thoughts

page 341:

• Curiously, evidence for the opposite point of view was being developed in Canada at roughly the same time that Lashley was doing his last work, in the late 1940’s. The neurosurgeon Wilder Penfield was examining the reactions of patients whose brains had been operated on, by inserting electrodes into various parts of their exposed brains, and then using small electrical pulses to stimulate the neuron or neurons to which the electrodes had been attached.

• Was this MKUltra?

page 344:

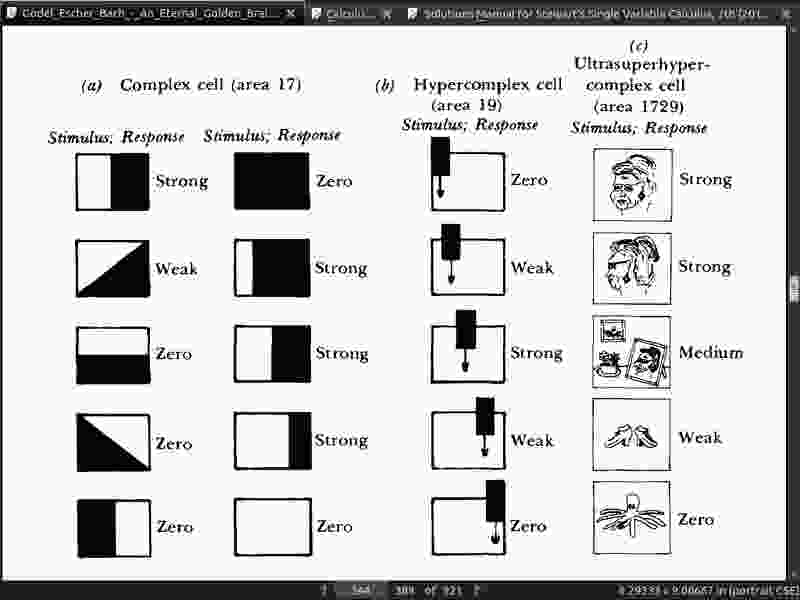
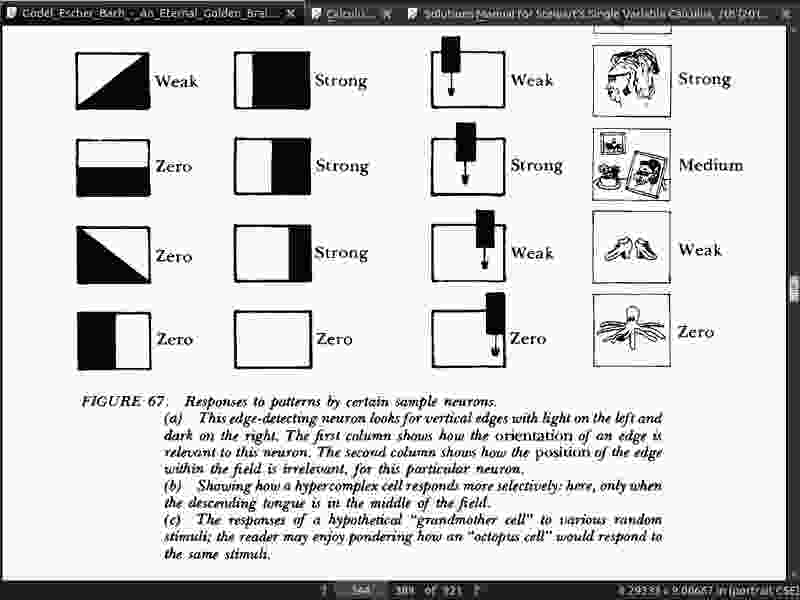
page 348:

• Let us from now on refer to these hypothetical neural complexes, neural modules, neural packets, neural networks, multineuron units-call them what you will, whether they come in the form of pancakes, garden rakes, rattlesnakes, snowflakes, or even ripples on lakes-as symbols.

page 357:

• Thus we are left with two basic problems in the unraveling of thought processes, as they take place in the brain. One is to explain how the low-level traffic of neuron firings gives rise to the high-level traffic of symbol activations. The other is to explain the high-level traffic of symbol activation in its own terms-to make a theory which does not talk about the low-level neural events. If this latter is possible-and it is a key assumption at the basis of all present research into Artificial Intelligence-then intelligence can be realized in other types of hardware than brains. Then intelligence will have been shown to be a property that can be “lifted” right out of the hardware in which it resides-or in other words, intelligence will be a software property.

page 359:

• Our facility for making instances out of classes and classes out of instances lies at the basis of our intelligence, and it is one of the great differences between human thought and the thought processes of other animals.

• A classic experiment with solitary wasps is reported in Dean Wooldridge’s book, Mechanical Man, from which I quote:

• When the time comes for egg laying, the wasp Sphex builds a burrow for the purpose and seeks out a cricket which ~he stings in such a way as to paralyze but not kill it. She drags the cricket into the burrow, lays her eggs alongside, closes the burrow, then flies away, never to return. In due course, the eggs hatch and the wasp grubs feed off the paralyzed cricket, which has not decayed, having been kept in the wasp equivalent of a deepfreeze. To the human mind, such an elaborately organized and seemingly purposeful routine conveys a convincing flavor or logic and thoughtfulness-until more details are examined. For example. the wasp’s routine is to bring the paralyzed cricket to the burrow, leave it on the threshold, go inside to see that all is well, emerge, and then drag the cricket in. If the cricket is moved a few inches away while the wasp is inside making her preliminary inspection, the wasp, on emerging from the burrow. will bring the cricket back to the threshold, but not inside, and will then repeat the preparatory procedure of entering the burrow to see that everything is all right. If again the cricket is removed a few inches while the wasp is inside, once again she will move the cricket up to the threshold and reenter the burrow for a final check. The wasp never thinks of pulling the cricket straight in. On one occasion this procedure was repeated forty times, always with the same result. 4

• This seems to be completely hard-wired behavior. Now in the wasp brain, there may be rudimentary symbols, capable of triggering each other; but there is nothing like the human capacity to see several instances as instances of an as-yet-unformed class, and then to make the class symbol; nor is there anything like the human ability to wonder, “What if I did this-what would ensue in that hypothetical world?” This type of thought process requires an ability to manufacture instances and to manipulate them as if they were symbols standing for objects in a real situation, although that situation may not be the case, and may never be the case.

English French German Suite

• Lewis Carroll’s nonsense, Jabberwocky, translated into French and German

· 12: Minds and Thoughts

Aria with Diverse Variations

· 13: BlooP and FlooP and Gloop

page 406:

• From here on out, the representability of all primitive recursive truths will be the criterion for calling a system “sufficiently powerful”.

• The significance of the notion is shown by the following key fact: If you have a sufficiently powerful formalization of number theory, then Godel’s method is applicable, and consequently your system is incomplete. If, on the other hand, your system is not sufficiently powerful (i.e., not all primitive recursive truths are theorems), then your system is, precisely by virtue of that lack, incomplete. Here we have a reformulation of “Ganto’s Ax” in metamathematics: whatever the system does, Godel’s Ax will chop its head om Notice also how this completely parallels the high-fidelity-versus-low- fidelity battle in the Contracrostipunctus.

Air on G’s String

· 14: On Formally Undecidable Propositions of TNT and Related Systems

page 456:

• Furthermore-and perhaps this is even more to the point-physicists do not study just the 3-D space we live in. There are whole families of “abstract spaces” within which physical calculations take place, spaces which have totally different geometrical properties from the physical space within which we live. Who is to say, then, that “the true geometry” is defined by the space in which Uranus and Neptune orbit around the sun? There is “Hilbert space”, where quantum-mechanical wave functions undulate; there is “momentum space”, where Fourier components dwell; there is “reciprocal space”, where wave-vectors cavort; there is “phase space”, where many-particle configurations swish; and so on. There is absolutely no reason that the geometries of all these spaces should be the same; in fact, they couldn’t possibly be the same! So it is essential and vital for physicists that different and “rival” geometries should exist.

• But an “abstract space” is not the real physical 3-D space of reality. These abstractions may allow for ease of understanding, but the math is not the territory.

• You fit your mathematics to the world, and not the other way around.

Birthday Cantatatata…

· 15: Jumping Out of the System

page 475:

• As the ordinals [names of infinities] get bigger and bigger, there are irregularities, and irregularities in the irregularities, and irregularities in the irregularities in the ir- regularities, etc. No single scheme, no matter how complex, can name all the ordinals. And from this, it follows that no algorithmic method can tell how to apply the method of Godel to all possible kinds of formal systems. And unless one is rather mystically inclined, therefore one must conclude that any human being simply will reach the limits of his own ability to Godelize at some point. From there on out, formal systems of that complexity, though admittedly incomplete for the Godel reason, will have as much power as that human being.

• But-one should not consider TNT defective for that reason. If there is a defect anywhere, it is not in TNT, but in our expectations of what it should be able to do. Furthermore, it is helpful to realize that we are equally vulnerable to the word trick which Godel transplanted into mathematical formalisms: the Epimenides paradox. This was quite cleverly pointed out by C. H. Whitely, when he proposed the sentence “Lucas cannot consistently assert this sentence.” If you think about it, you will see that (1) it is true, and yet (2) Lucas cannot consistently assert it. So Lucas is also “incomplete” with respect to truths about the world. The way in which he mirrors the world in his brain structures prevents him from simultaneously being “consistent” and asserting that true sentence.But Lucas is no more vulnerable than any of us. He is just on a par with a sophisticated formal system.

page 476:

• An amusing way to see the incorrectness of Lucas’ argument is to translate it into a battle between men and women … In his wanderings, Loocus the Thinker one day comes across an unknown object-a woman. Such a thing he has never seen before, and at first he is wondrous thrilled at her likeness to himself; but then, slightly scared of her as well, he cries to all the men about him, “Behold! I can look upon her face, which is something she cannot do-therefore women can never be like me!” And thus he proves man’s superiority over women, much to his relief, and that of his male companions. Incidentally, the same argument proves that Loocus is superior to all other males, as well-but he doesn’t point that out to them. The woman argues back: “Yes, you can see my face, which is something I can’t do-but I can see your face, which is something you can’t do! We’re even.” However, Loocus comes up with an unexpected counter: “I’m sorry, you’re deluded if you think you can see my face. What you women do is not the same as what we men do-it is, as I have already pointed out, of an inferior caliber, and does not deserve to be called by the same name. You may call it ‘womanseeing’. Now the fact that you can ‘womansee’ my face is of no import, because the situation is not symmetric. You see?” “I woman- see,” womanreplies the woman, and womanwalks away …

• Well, this is the kind of “heads-in-the-sand” argument which you have to be willing to stomach if you are bent on seeing men and women running ahead of computers in these intellectual battles.

page 477:

• Erving Goffman in his book Frame Analysis:

• For example, an obviously professional actor completes a commercial pitch and, with the camera still on him, turns in obvious relief from his task, now to take real pleasure in consuming the product he had been advertising. This is, of course, but one example of the way in which TV and radio commercials are coming to exploit framing devices to give an appearance of naturalness that (it is hoped) will override the reserve auditors have developed. Thus, use is currently being made of children’s voices, presumably because these seem unschooled; street noises, and other effects to give the impression of interviews with unpaid respondents; false starts, filled pauses, byplays, and overlapping speech to simulate actual conversation; and, following Welles, the interception of a firm’s jingle commercials to give news of its new product, alternating occasionally with interception by a public interest spot, this presumably keeping the faith of the auditor alive. The more that auditors withdraw to minor expressive details as a test of genuineness, the more that advertisers chase after them. What results is a sort of interaction pollution, a disorder that is also spread by the public relations consultants of political figures, and, more modestly, by micro-sociology.6

page 478:

• A Zen person is always trying to understand more deeply what he is, by stepping more and more out of what he sees himself to be, by breaking every rule and convention which he perceives himself to be chained by…

Edifying Thoughts of a Tobacco Smoker

page 519:

page 532:

page 534:

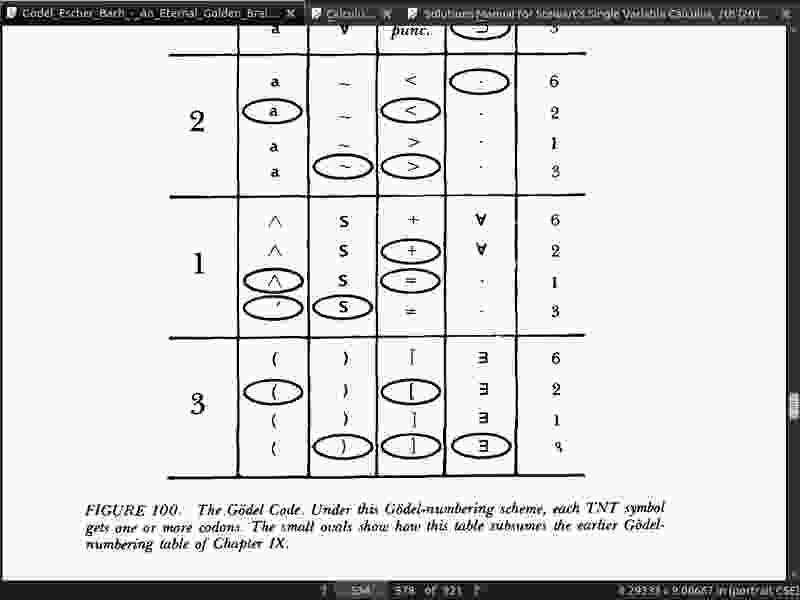
· 16: Self-Rep and Self-Rep

page 547:

• A natural and fundamental question to ask, on learning of these incredibly intricately interlocking pieces of software and hardware is: “How did they ever get started in the first place?” It is truly a baffling thing. One has to imagine some sort of a bootstrap process occurring, somewhat like that which is used in the development of new computer languages-but a bootstrap from simple molecules to entire cells is almost beyond one’s power to imagine. There are various theories on the origin of life. They all run aground on this most central of all central questions: “How did the Genetic Code, along with the mechanisms for its translation (ribosomes and tRNA molecules), originate?” For the moment, we will have to content ourselves with a sense of wonder and awe, rather than with an answer. And perhaps experiencing that sense of wonder and awe is more satisfying than having an answer-at least for a while.

The Magnificrab, Indeed

· 17: Church, Turing, Tarski, and Others

page 558:

• one of the main theses of this book: that every aspect of thinking can be viewed as a high-level description of a system which, on a low level, is governed by simple, even formal, rules.

page 569:

• According to my hypothesis, then, imagery and analogical thought processes intrinsically require several layers of substrate and are therefore intrinsically non-skimmable. I believe furthermore that it is precisely at this same point that creativity starts to emerge

page 570:

page 572:

SHRDLU, Toy of Man’s Designing

· 18: Artificial Intelligence: Retrospects

page 629:

• the top five words Artificial Intelligence: Retrospects of English-“the”, “of”, “and”, “a”, and “to”-would be equivalent to solving the entire problem of AI, and hence tantamount to knowing what intelligence and consciousness are. A small digression: the five most common nouns in English are-according to the Word Frequency Book compiled by John B. Carroll et al-“time”, “people”, “way”, “water”, and “words” (in that order). The amazing thing about this is that most people have no idea that we think in such abstract terms. Ask your friends, and 10 to 1 they’ll guess such words as “man”, “house”, “car”, “dog”, and “money”. And– while we’re on the subject of frequencies-the top twelve letters in English, in order, according to Mergenthaler, are: “ETAOIN SHRDLU”.

Contrafactus

• ‘What if’ playback on a subjunctive TV, subjuncTV

· 19: Artificial Intelligence: Prospects

Sloth Canon

· 20: Strange Loops, Or Tangled Hierarchies

page 708:

• My belief is that the explanations of “emergent” phenomena in our brains-for instance, ideas, hopes, images, analogies, and finally consciousness and free will-are based on a kind of Strange Loop, an interaction between levels in which the top level reaches back down towards the bottom level and influences it, while at the same time being itself determined by the bottom level.

Six-Part Ricercar

page 741:

• Author: I guess it all depends on how you look at it. But major or minor, I’d be most pleased to tell you how I braid the three together, Achilles. Of course, this project is not the kind of thing that one does in just one sitting-it might take a couple of dozen sessions. I’d begin by telling you the story of the Musical Offering, stressing the Endlessly Rising Canon, and-

• Achilles: Oh, wonderful! I was listening with fascination to you and Mr. Crab talk about the Musical Offering and its story. From the way you two talk about it, I get the impression that the Musical Offering contains a host of formal structural tricks.

• Author: After describing the Endlessly Rising Canon, I’d go on to describe formal systems and recursion, getting in some comments about figures and grounds, too. Then we’d come to self-reference and self- replication, and wind up with a discussion of hierarchical systems and the Crab’s Theme.