Home · Articles · 2016 · Graph Databases

TODO
- Use more markdown
- link networkx page
- Add a connecting/backlink from the oreilly graph book page
Python Algorithms: Mastering Basic Algorithms
page 23:
-
In many cases, if you can formulate what you’re working on as a graph problem, you’re (at least) halfway to a solution. And if your problem instances are in some form expressible as trees, you stand a good chance of having a really efficient solution.
-
Trees are just a special kind of graphs, so most algorithms and representations for graphs will work for them as well.
page 87:
- Such dependencies are (as mentioned in Chapter 2) easily represented as a directed acyclic graph (DAG), and finding an ordering that respect the dependencies (so that all the edges point forward in the ordering) is called topological sorting. Figure 4-5 illustrates the concept. PICTURE
G = (V,E), Where:
- G is a Graph
- V is a set of vertices (nodes)
- E is a set of edges (relationships)
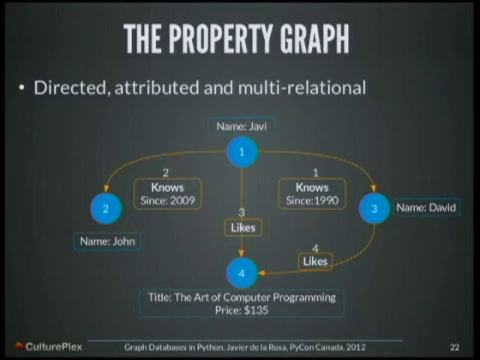
Vertices, or nodes, are often nouns, while the edges, or relationships, are often verbs. A person, John Smith, is a node. An address, 123 Main St., is also a node. John Smith “lives at” 123 Main St. designates a relationship (verb) between 2 nodes.
John Smith might “marry” Jane Smith, “know” Mr. George, and “work for” Boeing. Each of these edges can carry a weight as well as be directed or undirected. Multigraphs allow for multiple edges between nodes with different weights and attributes.
From youtube video: Graph_Databases_in_Python.


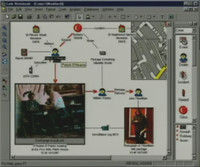
One especially important type of graph is the property graph. This is the type of graph to be used in a “detective” web application where users can help build a case against the global oligarchy.


- Bulbflow?
- PyBlueprints
- Gremlin


Database structure
- Single link between nodes
- Undirected
- Leave the naming of edges to the users, too many to predict
Nodes:
User
- username
- password
- joined
Person
- Name
Organization
- Name
Location
- Name
- Address
User Edges:
- Submitted (an edge)
- Updated (a node/edge’s info)
Edges:
- Lives_at
- Visited {date:2016-09-26}
- Married, dating, {since:2016-09-26}
- Employee_Of {title:“President”}
- Works_With {project:“sadf”}
- Member_Of {title:“Member”}
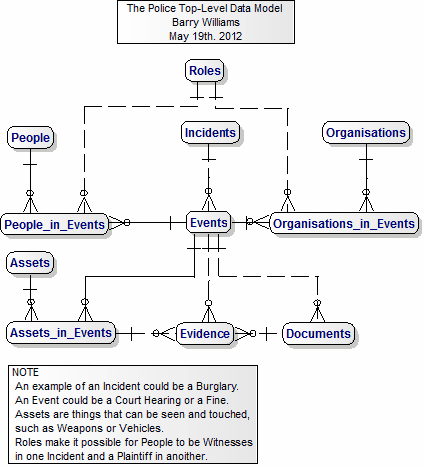
Sample SQL schemas from police dbs. These are good starting points for a relational database.
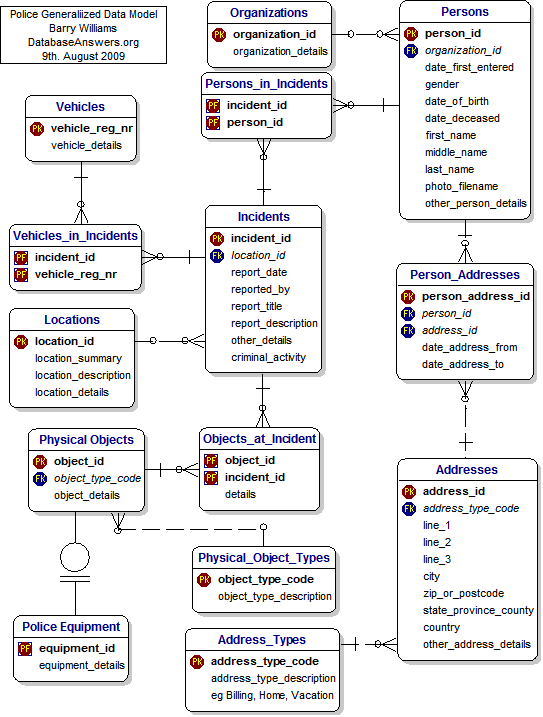
References:
-
Amit Patel provides shortest path algorithm information at www.redblobgames.com.
-
For more details on the specific graph database I use, check out the Neo4j page.